Как сделать развертку

Конус 1:20

Метрические конусы инструментов. Отверстия в шпинделях станков.

Конус Морзе – это одно из самых распространенных средств для закрепления инструмента на станке. Свое название данный инструмент получил в честь знаменитого инженера Стивена Морзе, жившего в XIX веке. Сегодня для правильного выбора размеров этого изделия применяют дробные числа. Существует несколько стандартизованных значений, различающихся углами наклона и размерами.

Читать также: Красностойкость быстрорежущих сталей это

Область применения конуса Морзе – это машиностроение. С его помощью можно быстро и очень точно закрепить режущий инструмент. Для этого конус Морзе крепится в станке в специальном отверстии или патроне, а в него в свою очередь вставляется например сверло. Такой способ крепежа гарантирует наиболее точное центрирование и последующую обработку. Также с его помощью можно подавать к обрабатываемой детали или режущему инструменту смазочно-охлаждающую жидкость.

Пример решения геометрической задачи

Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.

Задача не является сложной, если вспомнить, что круглый конус — это фигура вращения прямоугольного треугольника. Из этого треугольника следует однозначная связь между высотой, радиусом и образующей. Запишем соответствующую формулу:

Вторым выражением, которое следует использовать при решении, является формула для угла φ:

Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).

Выражаем из второй формулы g и подставляем результат в первую, получаем:

Угол φ = 120o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:

Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14 2 — 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Нормальные углы и конусы инструментов

НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )

&nbsp Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.

НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )

&nbsp Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

&nbsp Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )

&nbsp Стандарт распространяется на укороченные инструментальные конусы Морзе.

&nbsp *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. &nbsp ** размеры для справок.

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСА

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ( ГОСТ 25557-2006 )

&nbsp Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74.

&nbsp В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

&nbsp В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

BI — внутренний конус с пазом; BE — наружный конус с лапкой; AI — внутренний конус с отверстием по оси; АЕ — наружный конус с резьбовым отверстием по оси; BIK — внутренний конус с пазом и отверстием для подачи СОЖ; ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ; AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ; АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ( ГОСТ 25557-2006 )

КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )

&nbsp Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.

КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )

&nbsp Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

&nbsp Примечания: &nbsp 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. &nbsp 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

&nbsp Пример обозначения конуса Морзе 3, степени точности АТ8:

Морзе 3 АТ8 ГОСТ 25557-2006

&nbsp То же метрического конуса 160, степени точности АТ7:

Метр. 160 АТ7 ГОСТ 25557-2006

&nbsp То же укороченного конуса В18, степени точности АТ6:

Морзе В18 АТ6 ГОСТ 9953-82

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Для чего используется конус

Мы подробно разобрали самые простые варианты как сделать правильный конус из бумаги. Для чего используется эта поделка? Направления у нее самые различные:

• геометрических выставок;
• объемных поделок;
• изготовления маскарадных шляп.

Ваша фантазия подскажет вам, где еще может применяться конус. А мы поможем вам вдохновиться с помощью простой конусной поделки елочки.

Ёлка из конуса

Для нее потребуется:

• картон;
• бумага для подарков;
• скотч;
• декоративные предметы;
• ножницы.

В основе изделия, как вы уже поняли, лежит конус. Изготовьте его по одной из предложенных выше инструкций.

Далее работаем по схеме:

1. Полученный конус, оборачиваем бумагой для подарков. Крепим кончик материала к верхушке скотчем и аккуратно оборачиваем бумагу по фигуре. Отрезаем лишний материал.
2. Крепим концы с помощью скотча.
3. Вы не поверите, но елочка готова. Осталось ее украсить как настоящую. С этой целью могут подойти пуговицы, большие бусины и миниатюрные новогодние игрушки.

В ёлке можно сделать отверстия. И если она достаточно широка, поместите внутрь конуса новогодние огоньки. В темноте, они будут приятно мелькать, создавая приятную атмосферу.

http://ngeometry.ru/postroenie-razvertki-konusa.htmlhttp://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.htmlhttp://megamaster.info/kak-sdelat-konus-iz-bumagi/

Геометрическая задача

Необходимо провести расчет развертки усеченного конуса, который имеет высоту 13 см и радиусы оснований 2 см и 7 см.

Решение данной задачи с помощью непосредственного применения формулы для S невозможно, поскольку не известна длина генератрисы g. Тем не менее, ее можно вычислить, используя такую формулу:

Это выражение можно самостоятельно получить, рассмотрев прямоугольный треугольник со сторонами g, h и (R-r), здесь h — высота усеченного конуса. Генератриса g будет равна 13,93 см (значение приведено с точностью до 0,01 см).

Осталось подставить значения генератрисы и радиусов в формулу для S, чтобы получить требуемый ответ:

Следует не забывать, что записанная для S формула справедлива только для круглого прямого усеченного конуса.

Основные сведения о хвостовиках и их обозначение

Существует несколько видов исполнения инструментального конуса. Он может содержать резьбу, лапку или обходиться без них.

В его торце может быть нарезана резьба, которую делают для закрепления инструмента на шпинделе с использованием штревеля. Это специальный шток, предотвращающий выпадение инструмента. Также с его помощью изделие можно извлечь, если его случайным образом заклинит в шпинделе.

Если хвостовик изготовлен с лапкой, то она удерживает инструмент в шпинделе за счет того, что закреплена в специальном пазу. Лапка имеет два предназначения, с ее помощью легче достать изделие из шпинделя, а также создается жесткая фиксация и не будет проворачивания.

Также можно встретить исполнение с несколькими канавками и отверстиями. Они имеют разную глубину и размеры. Их задача – подводить к режущему инструменту смазочно-охлаждающую жидкость.

Хвостовики инструмента бывают различной конструкции и обозначаются буквенным кодом. Ниже приведена их расшифровка:

• BI – внутренний, имеется паз;
• ВЕ – наружный, имеется лапка;
• AI – внутренний, имеется отверстие по оси;
• АЕ – наружный, имеется отверстие по оси с резьбой;
• BIK – внутренний, имеются паз и отверстие для подачи смазочно-охлаждающей жидкости (СОЖ);
• ВЕК – наружный, имеется лапка и отверстие для подачи СОЖ;
• AIK – внутренний, содержит отверстия по оси и для подачи СОЖ;
• АЕК – наружный, содержит отверстие по оси с резьбой и отверстие для подачи СОЖ.

Наружный и внутренний соответствуют своим названиям. В зависимости от используемого инструмента, следует выбирать исполнение наружное или внутреннее.

Построение развертки трубы

Построение развертки трубы можно выполнить по аналогии с построением развертки усеченного конуса:

• построив трубу листовым телом;
• построив развертку Приложением Оборудование: Развертки

Если использовать первый способ, то усеченный конус мы строили командой «Линейчатая обечайка», а трубу нужно строить командой «Обечайка»

В остальном все очень похоже. Также создается эскиз на любой из системных плоскостей, например, на XY. Строится окружность. Запускается команда «Обечайка», указывается длина трубы и толщина стенки. Чертеж развертки получается опять же по аналогии с пошаговым описанием получения развертки усеченного конуса.

Если использовать способ с Приложением Оборудование: Развертки, но там понадобится команда «Патрубок цилиндрический тип 3». Указываются параметры трубы и получается развертка в автоматическом режиме.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Почему пожарные ведра имеют форму конуса?

Кто задумывался, почему пожарные ведра имеют, казалось бы, странную коническую форму? А это не просто так. Оказывается, коническое ведро при тушении пожара имеет много преимуществ перед обычным, имеющим форму усеченного конуса.

Во-первых, как оказывается, пожарное ведро быстрее наполняется водой и при переноске она не расплескивается. Конус, объем которого больше обычного ведра, за один раз позволяет перенести больше воды.

Во-вторых, воду из него можно выплеснуть на большее расстояние, чем из обычного ведра.

В-третьих, если коническое ведро сорвется с рук и упадет в огонь, то вся вода выливается на очаг возгорания.

Все перечисленные факторы позволяют сэкономить время — главный фактор при тушении пожара.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Определение диаметра через объем и высоту

Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:

Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:

Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:

Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.

Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.

Вы здесь

ОБРАБОТКА КОНИЧЕСКИХ ПОВЕРХНОСТЕЙ

§ 1. Общие сведения 1. Область применения конусов. Наряду с цилиндрическими деталями в машиностроении получили довольно широкое распространение детали с коническими поверхностями. Примерами их могут служить конусы центров, хвостовиков сверл, зенкеров, разверток. Для крепления этих инструментов передние участки отверстий шпинделя и пиноли токарного станка имеют также коническую форму. Однако область использования конусов не ограничивается режущими инструментами. Конические поверхности имеют многие детали машин. Широкое использование конических соединений объясняется рядом их преимуществ. 1. Они обеспечивают высокую точность центрирования деталей. 2. При плотном соприкосновении пологих конусов получается неподвижное соединение. 3. Изменяя осевое положение деталей конического соединения, можно регулировать величину зазора между ними. 2. Конус и его элементы. Конус представляет собой геометрическое тело, поверхность которого получается вращением прямой линии (образующей), наклонно расположенной к оси вращения (рис. 129, а). Точка пересечения образующей с осью называется вершиной конуса. Плоскости, перпендикулярные к оси конуса, называются, основаниями. Различают полный и усеченный конусы. Первый расположен между основанием и вершиной, второй — между двумя основаниями (большим и меньшим). Конус характеризуется следующими элементами: диаметром большего основания D; диаметром меньшего основания d; длиной l; углом уклона а между образующей и осью конуса; углом конуса 2а между противоположными образующими. Кроме этого, на рабочих чертежах конических деталей часто употребляют понятия конусность и уклон. Конусностью называется отношение разности диаметров двух перечных сечений конуса к расстоянию между ними. Она опреляется по формуле Уклоном называется отношение разности радиусов двух поперечных сечений конуса к расстоянию между ними. Его определяют по формуле Из формул (9) и (10) видно, что уклон равен половине конусности. Тригонометрически уклон равен тангенсу угла уклона (см. рис. 129, б, треугольник ABC), т. е. На чертеже (рис. 130) конусность обозначают знаком <, а уклон —, острие которых направляется в сторону вершины конуса. После знака указывается отношение двух цифр. Первая из них соответствует разности диаметров в двух принятых сечениях конуса, вторая для конусности— расстояние между сечениями, для уклона — удвоенной величине этого расстояния. Конусность и уклон иногда записываются числами десятичной дроби: 6,02; 0,04; 0,1 и т. д. Для конусности эти цифры соответствуют разности диаметров конуса на длине 1 мм, для уклона — разности радиусов на этой же длине. Для обработки полного конуса достаточно знать два элемента: диаметр основания и длину; для усеченного конуса — три элемента: диаметры большего и меньшего оснований и длину. Вместо одного из указанных элементов может быть задан угол наклона а, уклон или конусность. В этом случае для определения недостающих размеров пользуются вышеприведенными формулами (9), (10) и (11). Пример 1. Дан конус, у которого d=30 мм, /=500 мм, К=1: 20. Определить больший диаметр конуса. Решение. Из формулы (9) Пример 2. Дан конус, у которого D=40 мм, l = 100 мм, а=5 , Определить меньший диаметр конуса. Решение. Из формулы (11) По таблице тангенсов находим tg5°=0,087. Следовательно, d=40—2*100Х Х0,87=22,6 мм. Пример 3. Определить угол уклона а, если на чертеже указаны размеры конуса: D—50 мм, d=30 мм, /=200 мм. Решение. По формуле (11) Из таблицы тангенсов находим а=2 50 . Пример 4. Дан конус, у которого D=60 мм, /=150 мм, К=1 : 50. Определить угол уклона а. Решение. Так как уклон равен половине конусности, можно записать: По таблице тангенсов находим а=0 30 . 3. Нормальные конусы. Конусы, размеры которых стандартизованы, называются нормальными. К ним относятся конусы Морзе, метрические, конусы для насадных разверток и зенкеров с конусностью 1:50 0, под конические штифты — с конусностью 1:50, для конических резьб с конусностью 1 : 16 и др. Наибольшее распространение в машиностроении получили инструментальные конусы Морзе и метрические, основные размеры которых приведены в табл. 13.

Размеры конусов Морзе выражаются дробными числами. Это объясняется тем, что впервые стандарт на них был принят в дюймовой системе измерения, которая сохранилась до настоящего времени. Конусы Морзе имеют различную конусность (примерно 1 20), метрические конусы одинаковую — 1:20. Автор — nastia19071991

Что означает уклон в процентах, и как перевести его в градусы

Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.

Расчет уклона в процентах

Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.

Как понимать угол уклона в процентах?

Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.

Почему не в градусах?

Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами. Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.

Применение на практике

Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам. Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.

Круглый конус в геометрии

Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.

Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.

Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.

Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Значение конусности

Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:

1. Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
2. Для расчета примеряется следующая формула: i=AC/AB=tga.

Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.

Какую фигуру будем изучать?

Круглый прямой усеченный конус представляет собой два круга, имеющих разный диаметр, которые расположены в параллельных плоскостях. Окружности этих кругов соединены прямыми отрезками равной длины, именуемых образующими фигуры. Расстояние между круглыми основаниями называется высотой. Описанная фигура показана ниже на фото.

Получить ее можно двумя принципиально отличающимися геометрическими способами. Во-первых, можно взять обычный круглый конус и параллельной его основанию плоскостью отсечь верхнюю часть. Такое действие приведет к образованию верхнего (малого) основания усеченного конуса. Во-вторых, можно взять трапецию с двумя прямыми углами и вращать ее вокруг стороны, ограниченной этими углами. Сторона трапеции, вокруг которой будет происходить вращение, называется осью фигуры. Две параллельные стороны трапеции опишут круглые основания во время вращения, а четвертая наклонная сторона образует боковую поверхность фигуры.

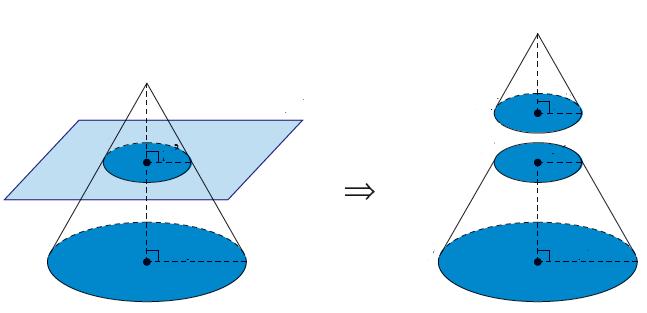
Схема выше демонстрирует получение усеченного конуса с помощью сечения плоскостью.