Калькулятор площади треугольника

Вы здесь

Онлайн калькулятор — Учеба и наука — Математика — Геометрия — Геометрический калькулятор — Треугольник

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Зная: Стороны треугольника	Зная: Два угла и сторону треугольника	Зная: Два угла и сторону треугольника «A»
Зная: Две стороны и угол треугольника	Прямоугольный треугольник	Зная: Катет и гипотенуза прямоугольного треугольника
Катет «B» и гипотенуза прямоугольного треугольника	Зная: Катет и угол прямоугольного треугольника	Катет «A» и угол «β» прямоугольного треугольника
Катет «B» и угол «α» прямоугольного треугольника	Катет «B» и угол «β» прямоугольного треугольника	Зная: Гипотенузу и угол прямоугольного треугольника
Гипотенуза и угол «β» прямоугольного треугольника	Равнобедренный треугольник	Зная: Высоту и сторону равнобедренного треугольника
Высота и сторона «B» равнобедренного треугольника	Зная: Сторону и угол равнобедренного треугольника	Сторона «A» и угол «β» равнобедренного треугольника
Сторона «B» и угол «α» равнобедренного треугольника	Сторона «B» и угол «β» равнобедренного треугольника	Зная: Высоту и угол равнобедренного треугольника
Высота и угол «β» равнобедренного треугольника	Равносторонний треугольник	Зная: Площадь равностороннего треугольника
Зная: Высоту равностороннего треугольника	Зная: Радиус вписанной окр. равностороннего треугольника	Зная: Радиус описанной окр. равностороннего треугольника
Зная: Основание и высоту треугольника

Метод Герона

Античный математик Герон Александрийский предложил свой способ получения квадратуры треугольника. Для вычислений достаточно знать длину трех его сторон, хотя сама методика достаточно сложна и не поддастся пятиклассникам:

1. Определите периметр: сложите отрезки сторон: a+b+c. Разделите число надвое. Полученные данные называются полупериметр (p) и имеют ключевое значение в геометрическом уравнении Герона.
2. Проведите вычисление по формуле: p (p — a) (p — b) (p — c). Т.е. сначала вычтите по отдельности длину каждой из сторон из значения полупериметра, а затем перемножьте между собой три полученных числа и сам полупериметр.
3. Извлеките корень из итогового значения. Искомая величина найдена.

Например, грани длиною 3, 4 и 5 см образуют полупериметр 6 см. После умножения согласно формуле получается значение 36. Корень из 36 равняется 6. Значит, 6 см2 — площадь этого треугольника. Для равносторонней фигуры расчет еще проще.

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².  В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.

Решение.

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60   

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два. 
S = 15 √3 / 2

Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

• AB- = (2−1; 5-(-3)) = (1; 8);
• BC- = (-2−2; -2−5) = (-4; -7).

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Предыдущая
ГеометрияВзаимное расположение двух плоскостей в пространстве — способы решения задач
Следующая
ГеометрияСложение векторов — свойства, правила и примеры решения задач

Как посчитать квадратные метры комнаты

В каких случаях требуется квадратура помещения:

• При установке на кухню модуля из шкафов.
• При оплате коммунальных услуг, где сумма рассчитывается исходя из метража.
• При оплате рабочим после ремонта. Их тарифы также привязаны к площадям и количеству метров.
• При определении нормативов освещения вычисляется площадь.
• При установке отопления, вентиляции и кондиционирования требуется знать объем (кубатуру) помещения. Он вычисляется с помощью величины площади.
• При расчете количества закупаемых материалов для планируемого ремонта.

Чтобы правильно высчитать необходимые величины нужно знать несколько формул и уметь с их помощью рассчитать квадратные метры стен, потолка и пола.

Квадратура помещения нужна при оплате коммунальных услуг, определении нормативов освещения, установке отопления и покупке материалов для ремонта.

Для этого потребуются простейшие инструменты:

• Рулетка. Механическая, размером от 3 до 5 метров. Ею измерять лучше вдвоем, чтобы избежать погрешностей. Минимальная единица измерения – миллиметр. Электронная, измеряет лазерным лучом. Получить измерительную величину можно просто направив луч в начальную точку. Единица измерения здесь – миллиметр или сантиметр.

  Некоторые «умные» рулетки могут сразу высчитывать площадь помещения, не измеряя дополнительно что-то. С измерениями такой рулеткой можно справиться в одиночку, без дополнительной помощи. Плюс в быстроте измерений и расчетов. Минус в дороговизне и проблемах с измерением неправильных помещений.

• Калькулятор. Также для удобства в расчетах разработаны специальные компьютерные программы.
• Угольник строительный. Должен быть с длинными сторонами – в этом случае замеры получатся более точными.
• Блокнот или тетрадь для занесения всех схем, измерений, расчетов.
• Уровень. С его помощью можно рассчитать отклонения вертикали/горизонтали.

Прежде чем приступить к измерениям и расчетам, нужно подготовить все необходимые инструменты.

1. Первое, что нужно сделать – это узнать, как рассчитывается квадратный метр. Здесь пригодится рулетка со шкалой в сантиметрах и метрах.
2. Затем измеряется длина помещения и его ширина. Причем, ширина измеряется, прикладывая рулетку строго перпендикулярно длине.
3. Измерения записываются вплоть до сантиметра. В сторону метров округлять не стоит.

Для измерения размеров помещения нужна обычная рулетка. Но существуют и “умные рулетки”. Они могут сразу высчитывать общую площадь.

Чтобы рассчитать квадраты на калькуляторе, нужно измеренную величину записать следующим образом: 1м=0.01 см. Если предположить, что длина комнаты – 3 метра 56 см, то на калькуляторе набрать 3,56. То же самое касается и ширины. В итоге, умножить длину комнаты на ее же ширину и получить величину квадратуры измеряемого помещения.

Для расчетов вам понадобится калькулятор и знание формул.

Для того, чтобы корректно измерить помещение, желательно освободить хотя бы две ее стороны от мебели и лишних предметов. В этом случае идеально измерять комнату на стадии ремонта.

Рулетка должна хорошо прилегать к измеряемой поверхности. Длину требуется измерить вдоль стены (или стен, если форма измеряемой фигуры не правильная). В начале измерений лучше проверить прямоугольность, измерив рулеткой диагонали помещения и сравнив цифры. Таким образом уточняется правильность формы.

Можно воспользоваться лазерной рулеткой. Такие дальномеры стали незаменимыми помощниками специалистов и умеют запоминать измерения и вычислять по ним площадь или кубатуру помещения.

А вот чтобы проверить прямые линии понадобится уровень. Реже большой строительный угольник или самодельный циркуль.

Уровень – инструмент для оценки соответствия поверхностей вертикальной и горизонтальной плоскости относительно земли.

Расчеты можно сразу переносить на схему. Обязательно измерять помещение несколько раз, во избежание ошибок. Во время замеров быть внимательным и собранным, следить абсолютно за всеми мелочами, которые могут повлиять на величины.

Площадь комнаты можно вычислить с помощью простой школьной формулы:

S=A*B.

• S – площадь;
• A – длина;
• B – ширина.

Подобным же образом можно вычислить и площадь каждой стены, пола и потолка.
В случае если помещение треугольной формы – нужно измерить длину и ширину, умножить друг на друга и разделить на 2.

Или по формуле:

S = (А*В)/2.

Площадь комнаты можно вычислить с помощью простой школьной формулы.

Классические методы расчета

Отличие в разных формулах заключается в исходных данных. В них используются различные элементы треугольника. В задачах не всегда есть возможность выбирать вводные величины. Базовая школьная формула основаны на знании длины одной из сторон (a):

• из противоположного угла на известное основание опускают высоту (h);
• измеряют ее длину;
• произведение двух известных величин делят надвое и получают площадь треугольника.

На заметку! Запись этой формулы:

Также в школьной программе часто используется способ расчета площади произвольного (в т. ч. равнобедренного) треугольника на основании известного угла (α) и длины примыкающих к нему сторон (a и b):

1. Вычислите синус угла.
2. Перемножьте между собой длины сторон.
3. Разделите величину надвое.
4. Умножьте друг на друга данные из пунктов 1 и 2. Результат готов.

На заметку! Запись данной формулы: 

В примере с прямоугольным треугольником посчитать его площадь можно в три нажатия на калькуляторе. Достаточно перемножить значения его катетов (прилегающих к прямому углу сторон) и разделить произведение надвое.

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение.

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )  (см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S₂ = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) ) (см. вторую строку на рисунке внизу)

Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S₂ = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка
S₂ = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня    
S₂ = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
S₂ = 4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) (см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

S₂ / S = 16 (см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)

На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)

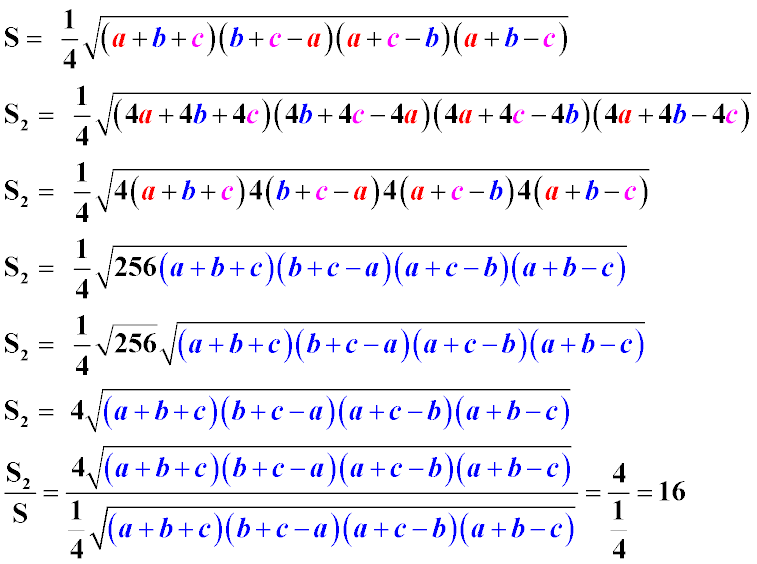
Ответ: Площадь треугольника увеличится в 16 раз

10380.6235
 

Сумма углов треугольникаОписание курса Медиана треугольника   

Для прямоугольного треугольника

В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.

По двум сторонам

Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:

\(S=\frac{a\times b}2\)

где a и b — катеты прямоугольного треугольника.

Через гипотенузу и острый угол

Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.

Начнем с поиска катета:

\(\cos\left(\alpha\right)=\frac ac\)

\(a=c\times\cos\left(\alpha\right)\)

где c — гипотенуза треугольника, a — его катет, а α —угол между ними.

Подставляем получившееся значение в формулу \(S=\frac12a\times c\times\sin\alpha\), получается:

\(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\)

Через катет и прилежащий угол

В этом случае нужно будет использовать следующую формулу:

\(S=\frac12\times a^2\times\tan\left(\alpha\right)\)

Через радиус вписанной окружности и гипотенузу

Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:

\(S=r\times(r+c)\)

где r — радиус вписанной окружности, c — гипотенуза.

Через вписанную окружность

Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:

\(S=с_1\times с_2\)

где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.

По формуле Герона

Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:

\(S=(p-a)\times(p-b)\)

где \(p=\frac{a+b+c}2\) — полупериметр фигуры.

Для равнобедренного треугольника

Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.

Через основание и сторону

 В этом случае формула будет выглядеть следующим образом:

\(S=\frac b4\sqrt{4a^2-b^2}\)

где a — одно из боковых ребер фигуры, а b — ее основание.

Через основание и противолежащий угол

Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:

\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)

где b — основание многоугольника, β — противолежащий ему угол.

Через основание и высоту

Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:

\(S=\frac{b\times h}2\)

где b — основание фигуры, а h — высота, проведенная к этому основанию.

Через боковые стороны и угол между ними

Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:

\(S=\frac12a^2\times\sin\left(\beta\right)\)

где a — это боковое ребро, β — угол между равными ребрами.

Через основание и угол между боковыми сторонами

В этом случае нам сначала придется найти высоту по формуле:

\(h=\frac b2\tan\left(\beta\right)\)

где β — угол при вершине, а b — основание.

Далее подставляем значение в формулу

\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)

Итоговая формула:

\(S=frac{b^2\tan\left(\beta\right)}4\)

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• длины катетов a и b
• длину гипотенузы с и длину любого из катетов (a или b)
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a = Катет b = S =

Просто введите длины двух катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c = Катет (a или b) = S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = ° S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету b — ∠α

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = ° S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b — ∠β

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Вычисления с помощью окружностей

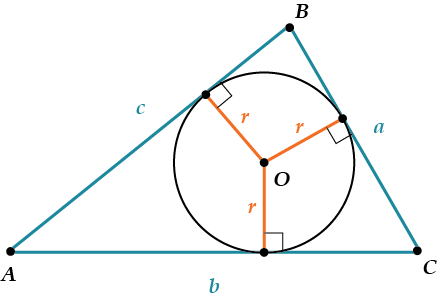
На практике используются способы расчета площади треугольника с помощью вписанной или описанной окружности. В первом случае необходимо знать величины всех сторон и радиус вписанного элемента. Далее:

• найдите полупериметр (p);
• умножьте полученную величину на значение радиуса (r) окружности и получите площадь.

Совет. При неизвестном радиусе его рассчитывают по формуле: r = P/2π. P — длина окружности, π — математическая константа.

По описанной вокруг треугольника окружности также можно вычислить его площадь. Потребуется знать радиус:

• получите произведение всех сторон треугольника;
• умножьте радиус на 4;
• разделите первое значение на второе.

Важно! Формула:

Пример для треугольника со сторонами 3,4 и 5 см. Если описать окружность, касающуюся каждой его вершины, то ее радиус будет равняться 2,5. После подстановки величин в уравнение получите итоговое значение 6 см2.

Предложенный набор методов — базовый, но вовсе не исчерпывающий. Существуют более сложные способы решения задания с меньшим количеством вводных данных и многоступенчатым расчетом.

Вычисляем метраж

Основные этапы работы:

1. Расчет производится вдоль стен комнаты. Поэтому предварительно рекомендуется освободить их. Для этого нет необходимости полностью освобождать комнату. Во многих случаях достаточно лишь отодвинуть предметы к центру помещения.
2. Измерение значения длины стены. Для этого понадобится рулетка. Ее прикладывают к углу одной из стен и закрепляют. Ведя рулетку вдоль стены до ее конца, находят значение длины.
3. Полученное значение следует записать на листе бумаги.
4. Таким же образом необходимо найти длину второй стены.
5. Полученные в результате измерения данные следует умножить между собой. Для этого можно воспользоваться калькулятором.

Найденные данные и являются метражом комнаты.

Чтобы найти площадь комнаты, не обязательно прибегать к услугам специалистов. Процедура достаточно проста и вполне доступна каждому. Следуя предложенным рекомендациям, можно без особых усилий и в короткие сроки получить необходимые значения площади помещения.

Начиная любой ремонт, вам нужно знать, как рассчитать площадь комнаты. Эти знания помогут вам подобрать правильное количество материалов, а также грамотно просчитать габариты. Такие знания необходимы и при приобретении недвижимости, когда нужно проверить указанную в документах площадь.

Наш обзор поможет вам вспомнить школьные знания и подскажет, как применить их на практике. Кроме того, вы сможете воспользоваться специальным калькулятором.

При расчете площадей потолка, пола и стен, необходимо выяснить, как рассчитать квадратный метр. Для вычислений необходимо выбрать мерную ленту или рулетку с нанесением делений в сантиметрах или метрах. Такое приспособление применяются для площади в квадратных метрах.

Если величина получается больше метра, то используются не только метры, но и сантиметры.

Чтобы правильно провести расчеты можно воспользоваться калькулятором квадратных метров. При необходимости померить всю длину, можно делать это поэтапно. Например, сделать отметку там, где закончилась рулетка, а затем протянуть ее еще раз.

Ширина меряется также рулеткой. При этом ее располагают под углом в 90 градусов к длине. Если длина меньше метра, то необходимо округлить в сторону ближайшего сантиметра.

При расчете квадратных метров калькулятором, не всегда получается выполнить измерения в метрах. Показатель отображается, как в метрах, так и в сантиметрах. При этом 1 см равняется 0,01 метра. Например, 98 см равно 0,98 м. То есть можно записать 2,98 м. Чтобы получить площадь нужно длину умножить на ширину. Округлять значение можно в большую сторону.

Стоит отметить и другие единицы измерения:

• в 1 квадратном фунте – 0,093 квадратных метра;
• в ярде – 0,84 кв. м.

требуется точный расчет материалов для ремонта;
наемные мастера часто проводят расчеты оплаты за квадратный метр, что необходимо перепроверять для исключения обмана;
необходимы знания расчетов при выборе площади

Часто оплата коммунальных услуг вычисляется, исходя из размеров комнаты;
чтобы определить нормативы освещенности также нужно знать габариты помещения;
зная площадь, всегда можно посчитать объем, что очень важно при установке отопительных, вентиляционных и климатических устройств.. В ролике дается простое объяснение необходимых значений:

В ролике дается простое объяснение необходимых значений:

Площадь треугольника формула

*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.

Формула вторая

Как уже было изложено в статье о площади параллелограмма формула имеет вид:

Площадь треугольника равна половине его площади, значит:

*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.

Формула Герона (третья)

Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.

*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.

Формула четвёртая

где r – радиус вписанной окружности

*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.

Формула пятая

где R – радиус описанной окружности.

*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.

Возникает вопрос: если  известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!

Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются  в составе ЕГЭ.

Давайте отдельно рассмотрим формулу:

Она является частным случаем формулы площади многоугольника, в который вписана окружность:

Рассмотрим её на примере пятиугольника:

Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём  опущенные перпендикуляры являются радиусами вписанной окружности:

Площадь пятиугольника равна:

Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:

Формула шестая

Пусть сторона треугольника равна a, из противоположной вершины к этой стороне проведён произвольный отрезок образующий с ней угол (фи):

Тогда

Данная формула используется очень редко на практике, возможно вы её видите впервые, ну так просто написал, чтобы знали. Её ещё можно вывести преобразовав формулу площади четырёхугольника:

Также она является следствием из :

Что добавить? Есть ещё формулы треугольника связанные с координатами  вершин, векторами на которых он построен. Об этом будет статья в будущем, не пропустите!

Площадь прямоугольного треугольника. Тут всё просто — она равна половине площади прямоугольника, то есть одной второй произведения катетов.

На этом всё! Успеха Вам!

Калькулятор онлайн.Вычисление площади треугольника

Этот математический калькулятор онлайн поможет вам вычислить площадь треугольника. Программа для вычисления площади треугольника не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.

А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные. Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.

В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.

Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.

В качестве числителя, знаменателя и целой части дроби может выступать только целое число. Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления:

Ввод: -2/3 Результат: ( -frac{2}{3} )

Целая часть отделяется от дроби знаком амперсанд: &

Ввод: -1&5/7 Результат: ( -1frac{5}{7} )

1 Общие формулы для вычисления площади треугольника

Формула площади треугольника по длине и высоте

S= a*h/2,
где а – это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.

Формула Герона

S=√р*(р-а)*(р-b)*(p-c),
где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.

S = (a*b*sin(α))/2,
где b,c -это длина сторон треугольника, sin(α)- синус угла между двумя сторонами.

Формула площади треугольника по радиусу вписанной окружности и трем сторонам

S=p*r,
где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.

Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности

S= (a*b*c)/4*R,
где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.

Формула площади треугольника по декартовым координатам точек

Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
S = |(x1 – x3)•(y2 – y3) – (x2 – x3)•(y1 – y3)|/2,
где || обозначает модуль.

Как снизить количество отходов

Для решения этого вопроса есть, наверное, единственный способ. Как известно, все полотна выпускаются производителями определенного размера, но есть фирмы, которые выполняют нарезку листов по заданному размеру.

Можно точно отмерив, сделать заказ, который также будет покрыт защитным верхним слоем на местах срезов. В этом случае можно застелить даже 8 метровые полотнища, с вызовов специалиста, который подрежет все на месте.

Такой способ значительно сократит отходы, а также благодаря профессиональным действиям специалистов можно не беспокоиться о понижении эксплуатационных характеристик кровельного покрытия.

К недостатку этого метода можно отнести следующие моменты:

• полотна длиной свыше 5 метров сложнее транспортировать и хранить, в отличие от обычных;
• металлочерепица такой длины также сложна в установке и подъеме;
• стоимость будет немного больше, чем при самостоятельном монтаже, так как за дополнительную услугу придется заплатить.

Площадь треугольника

Треугольник имеет три угла или вершины, и три стороны, которые являются прямыми отрезками.

Равносторонним треугольником является треугольник, который имеет равную длину всех трех сторон.

Если две стороны треугольника и два прилегающих к ним угла равны между собой — такой треугольник называется равнобедренным

Формулы площади треугольника:

• Площадь треугольника = a * h/2
• Периметр треугольника = a + b + c
• Площадь равностороннего треугольника = (√(3) / 4) * a²
• Площадь равнобедренного треугольника = ½ * a * b * SinC

где,

• h — высота треугольника,
• a, b, c = стороны треугольника

Примеры :

Задача 1: Найдите площадь треугольника у которого высота = 3, а длина основания = 4.Шаг 1: Найдем площадь.Площадь = h * b/2 = 3 * 4/2 = 12/2 = 6.

Задача 2: Найдите периметр треугольника, если известна длина его трех сторон = 1, 2, 3.

Шаг 1: Найдем периметр.Периметр = a + b + c = 1 + 2 + 3 = 6.

Задача 3: Найдите площадь равностороннего треугольника, если длина его стороны равна 3.

Шаг 1: Найдем площадь.Площадь = (√(3) / 4) * a² = (1.73 / 4) * 3² = 0.43 * 9 = 3.87.

Задача 4: Найдите площадь равнобедренного треугольника если сторона его равна 3, основание = 4 и угол между ними 28.

Шаг 1: Найдем площадь.Площадь = ½ * a * b * SinC = 0.5 * 3 * 4 * Sin(28) = 6 * 0.27 = 1.62.

Приведенные выше примеры показывают, как вычислить площадь и периметр треугольника, равностороннего треугольника,равнобедренного треугольника вручную.