Существует ли треугольник

Описание треугольников

Начиная писать любую статью, хочется сделать ее, прежде всего уникальной и неповторимой. Подписчики моего сайта, должны находить ответы на все свои вопросы в моих статьях. По этой причине, приходится перечитывать кучу литературы и статей с аналогичных моему сайтов.

В итоге оказывается, создать уникальную статью совсем не сложно. К сожалению, практически все владельцы форекс сайтов, скачивают информацию друг у друга, и практически все статьи как под копирку. Конечно это возмущает, не уж то нет своей головы, но да ладно, вернемся к теме.

Практически во всех книгах, и на всех сайтах, трейдеры сходятся во мнении, что фигура графического анализа треугольник — фигура неопределенности. И хотя ее классифицируют, как фигуру продолжения тренда, не всегда это срабатывает.

Виды треугольников

Всего имеется 4 вида треугольников, одна из них разворотная фигура, и три фигуры продолжения тренда. Надо понимать, что все это условно и к каждой сделке, нужно подходить индивидуально.

К разворотным фигурам, относится:

расходящийся треугольник.

К фигурам продолжения, относятся:

• симметричный треугольник;
• нисходящий треугольник;
• восходящий треугольник.

Построение треугольника

Построить любой из выше перечисленных треугольников, можно всего лишь по 4 точками.

По такому же принципу, строятся и остальные виды треугольников. В случае симметричного, нисходящего и восходящего треугольников, обязательное правило, линии должны сходились, для расширяющегося треугольника, расходились.

Пробой треугольника

В различных книгах по техническому анализу пишут: «Выход из треугольника, в большинстве случаев будет противоположный от входа». Это значит, если до начала формирования треугольника, тренд был вверх, то и выход из треугольника будет вверх (исключение, расходящийся треугольник). Но, в тех же книгах по трейдингу, встречаются фразы по типу: «Нельзя заранее определить в какую сторону будет выход». 

Поэтому предлагаю не гадать, а использовать единственно верный метод, дождаться выхода (пробоя) и следовать за ценой.

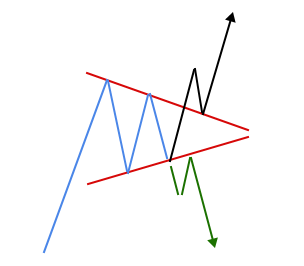
Если мы видим, что цену зажимают в фигуру технического анализа Треугольник, то чего нам торопиться? Цена никуда не убежит, есть время подождать. А вот когда произойдет пробой треугольника, это наш сигнал в какую сторону собирается двигаться рынок. Здесь то и можно вступать в игру. Входим на ретесте пробитого уровня, и торгуем по тренуд.

Где ставить take profit? 

Не решенным остался только один вопрос, где ставить take profit? 

Для расчета профита, нужно отложить максимальную ширину треугольника, от места пробой. Заложитесь на несколько пунктов в меньшую сторону и ждать тейка.

Треугольник

Издавна фигура соотносилась с огнем, горой, камнем, вершиной, отражала связь мира земного и горнего. Перевернутая вершиной вниз фигура олицетворяла древнейшую Великую Богиню, подательницу небесных вод.

В зависимости от положения вершины, изображение означает женское или мужское начало, а две совмещенные фигуры символизируют созидание и творческую силу. Перевернутый треугольник уподоблялся чаше и Святому Граалю, вершиной вверх — сердцу.

Как первейший символ триединства фигура чаще всего отражала небо, землю и между ними человека либо сущность божественную, человеческую, животную.

Треугольник также обозначал мир мертвых, живых и высших сфер.

1. У древних египтян вертикальная сторона треугольника отождествлялась с мужчиной (начало), горизонтальная — с женщиной (середина, хранилище), гипотенуза — с потомством (завершение). В мире богов эти основы продолжения рода представляла триада Озириса, Изиды и Гора. Египтяне считали природой всего сущего и совершенством число три, содержащееся в треугольнике, священное соотношение сторон и гипотенузы которого соответствовало соотношению 3:4:5.
2. В античных Афинах правильный треугольник был посвящен богине знания и мудрости Афине, а также символизировал космос, созидание, абсолют и считался божественным творением. Тетрактис Пифагора, содержащий десять точек и девять равносторонних треугольников, отождествлялся с Великим Единосущным, содержащим в себе все остальное.
3. В христианстве фигура символизирует Троицу и в качестве треугольного нимба является атрибутом Бога-Отца. Так называемый щит Святой Троицы в виде перевернутого треугольника нередко является частью витражей готических соборов. В период Возрождения треугольник с божественным всевидящим Оком изображался как знак высшего проведения, а позже стал частью масонской символики. Глаз Бога, изображенный в треугольнике, также является символом Иеговы в иудаизме и присутствует в культовом изобразительном искусстве Древнего Египта.

Существуют иные фигуры, образующие три равные стороны. Период и места их происхождения отличаются, но в христианстве значение символа триединства для этих знаков остается аналогичным — они все отождествляют Святую Троицу.

Татуировка

Такое тату – универсально. Оно нравится и мужчинам, и женщинам. Первые любят набивать его на руке. Дамы предпочитают более закрытые места: спина, бедро, икры ног.

При набивке пары треугольников, особенно тех, которые имеют пересечения, для многих это – выражение победы Духа над всем, что несет в себе телесное. В другом случае символизируются во взаимодействии две противоположные стихии: Огонь (треугольник с вершиной вверх) и Вода (перевернутая фигурка).

Иудеи такому тату придают несколько иное значение, а именно: верность мышления, наполненность словами, выполнение дела. Христиане связывают с триединством Божественных начал.

Рекомендуем посмотреть видео — «Печать Соломона»:

Подписывайтесь на нашу интересную группу Вконтакте:

Поделиться с друзьями:

Элементы остроугольного треугольника:

Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.

Рис. 4. Остроугольный треугольник и внешний угол

∠ ВСD – внешний угол

Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника

MС – медиана остроугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 6. Остроугольный треугольник и высота остроугольного треугольника

MС – высота остроугольного треугольника

Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.

Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника

MС – биссектриса угла остроугольного треугольника

Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Свойства треугольников

Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.

Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.

Определение 9

Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.

Определение 10

Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.

Определение 11

Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.

Теорема 1

Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.

Теорема 2

Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.

Теорема 3

Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.

Следующие две теоремы рассматривают свойства для равнобедренных треугольников.

Теорема 4

Углы при основании равнобедренного треугольника будут равными.

Теорема 5

Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.

Замечание 1

Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.

Треугольник Кеплера

В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника, который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.

Великий треугольник соединения Сатурна и Юпитера

Четыре стихии: Земля, Вода, Воздух и Огонь. Миниатюра из алхимического трактата XVII в.

Рождение Сына Солнца из Философского яйца. Миниатюра из алхимического трактата XVII в.

Король Земли поклоняется философской сере. Миниатюра из алхимического трактата XVII в.

Тупоугольный треугольник (понятие и определение):

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов

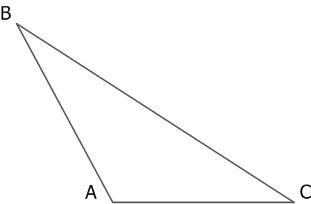
Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

∠ АВС, ∠ BСA – острые углы треугольника

По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник, т.к. у него каждый угол составляет 60°.

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника 

По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.

Рис. 3. Прямоугольный треугольник

Тупоугольный треугольник также может быть одновременно равнобедренным треугольником. Но не всякий равнобедренный треугольник тупой.

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

∠ ВАС – вершинный угол, ∠ АBC и ∠ BСA – углы при основании

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

[править] Типы треугольников

Треугольники можно классифицировать в зависимости от относительной длины его сторон:

• В равностороннем треугольнике все стороны имеют одинаковую длину. Все углы равностороннего треугольника также одинаковы и равны 60°. Равносторонний треугольник еще называют правильным.
• В равнобедренном треугольнике две стороны имеют одинаковую длину, третья сторона при этом называется основой треугольника. Равнобедренный треугольник имеет два одинаковых угла, которые находятся при его основе.
• Разносторонний треугольник имеет стороны разной длины. Внутренние углы разностороннего треугольника разные.

Также треугольники можно классифицировать в соответствии с их внутренними углами:

• Прямоугольный треугольник имеет один внутренний угол равный 90° (прямой угол). Сторона, противоположная прямому углу, называется гипотенуза. Другие две стороны называются катетами прямоугольного треугольника.
• Тупоугольный треугольник имеет один внутренний угол больше 90°.
• В остроугольном треугольнике все углы меньше 90°. Равносторонний треугольник является остроугольным, но не все остроугольные треугольники равносторонние.

Треугольник Рёло — это выпуклый криволинейный треугольник, получаемый при пересечении трёх окружностей одного радиуса с центрами в вершинах правильного треугольника со стороной равной радиусу.

Что это такое?

Треугольником называется музыкальный инструмент с палочкой в комплекте, который относится к числу самых элементарных ударных. Своё название он получил из-за своей формы в виде равностороннего треугольника. В народе на Руси его называли не иначе как «трензель», однако столь необычное название в оркестре не прижилось.

В целом этот инструмент представляет собой прут из металла, который изогнут в нужную форму. При этом в одном из углов этого треугольного инструмента концы металлического прута не сходятся, то есть получается, что этот угол остаётся открытым.

Несмотря на визуальную простоту инструмента, производят его по строгим правилам, дабы не исказить его звучания. Для его создания задействуют особый вид стали – серебрянку

Большое внимание уделяют и палочке инструмента

Древнее происхождение

Некоторые знаки появились задолго до нашей эры, и точно определить их первоначальное значение теперь практически невозможно. Древнейшим символом триединства стало изображение треугольника, которое можно наблюдать в виде вырезов на кости и рисунков на первой керамике каменного века.

Со временем появлялись круги, точки, спирали, другие фигуры, составлявшие окружность или треугольник. Не всегда подобные рисунки имели какое-либо значение, чаще всего они были просто орнаментом. Порой такие изображения отмечали места культов и погребений.

С развитием богатой мифологии и организованной религии древних египтян, шумеров, греков, кельтов, иранских и других народов некоторые знаки стали священными. Они символизировали триады богов или ипостаси одного божества, трех его качеств и проявлений, обозначали мир высший, человеческий, подземный, процесс от рождения до смерти, а также другие представления о мироздании.

В период формирования античной философии, астрономии, геометрии знаки триад обрели дополнительное значение.

Целое, состоящее из трех частей, означало человеческие качества, состояния, действия, природные явления, стихии, небесные объекты, временные соотношения, виды искусства, математические функции, другие понятия. Появились визуальные варианты пересекающихся элементов треугольных форм и сочетания их с другими геометрическими фигурами.

Вариации символа были найдены в ходе многочисленных археологический раскопок. Мистический символ часто встречался с тремя головами, завязанным ртом или глазами. Эти разновидности талисмана можно отнести к символизму. Данные обереги напоминают о том, что нельзя полагаться и оценивать происходящее лишь по внешнему облику, необходимо понять суть, и только после этого делать выводы.

Также призывают осознать единство Тела и человеческой Души. Огромное значение для каждого человека имеют его собственные мысли и поступки. Необходимо стремиться к правильному образу жизни, включающему добрые помыслы и искреннее отношение к окружающим, только тогда может наступить мир и гармония.

Внимание также нужно уделять саморазвитию, оно поможет постичь много нового и является достижением мудрости

Знамя Мира

У символа из трех кругов или точек очень широкая область интерпретаций, во многом аналогичная с равносторонним треугольником. Самым известным вариантом знака стало Знамя Мира, дизайн которого был разработан русским художником, философом и писателем Рерихом Николаем Константиновичем для международного Пакта защиты культурного наследия в 1935 году.

Описание и цель применения символа в официальном договоре приводится таким образом:

О том, насколько знак распространен в религиозной культуре разных народов и что вдохновило художника на идейное и визуальное содержание Знамени Мира, сам Рерих говорит в своих письмах и записях, изданных в двухтомном собрании «Листы дневника»:

[править] См. также

По числу вершин	1-10 Одноугольник • Двуугольник • Треугольник • Четырёхугольник (Дельтоид) • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Десятиугольник 11-20 Одиннадцатиугольник (англ.) • Двенадцатиугольник • Тринадцатиугольник • Четырнадцатиугольник
Правильные	Выпуклые Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • … • 17-угольник • … • 257-угольник • … • 65537-угольник Звёздчатая форма Звезды (Пентаграмма • Гексаграмма • Октаграмма)
Выпуклые	Четырёхугольники: Параллелограмм • Прямоугольник • Ромб • Трапеция
Невыпуклые	Контрпараллелограмм
Теория и практика	Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Первый признак равенства треугольников

Теорема:

Два треугольника равны, если у них равны две стороны и угол, лежащий между этими сторонами.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

 AB = A₁B₁,  AC = A₁C₁,  ∠A = ∠A₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить  A₁B₁C₁  на  ABC  так, чтобы точка  A₁  совместилась с точкой  A  и сторона  A₁B₁  совместилась со стороной  AB,  то точка  B  совместится с точкой  B₁,  так как  A₁B₁ = AB.  Сторона  A₁C₁  совместится со стороной  AC,  так как  ∠A = ∠A₁.  Точка  C₁  совпадёт с точкой  C,  так как  A₁C₁ = AC.  Стороны  B₁C₁  и  BC  совместятся, так как совместились их концы. Таким образом, треугольники совместятся. Теорема доказана.

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства.

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

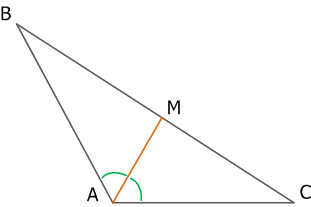
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Валькнут в руническом круге

Как было сказано выше, руны, расположенные вокруг валькнута, могут менять его значение.

Как правило, этот символ и изображается в окружении рун. Обычно это Дагаз, Турисаз, Уруз и Феху.

Данные руны циклично повторяются, что символизирует прибавление опыта со временем, а также развитие при постоянном продвижении.

При этом положение знака по отношению к руническим символам может иметь 8 вариантов (вариант определяется в зависимости от тех рун, на которые указывают выступающие углы валькнута), отчего изменяется значение оберега валькнут.

Вот смысл рун, в круг которых заключается рассматриваемый знак:

• Феху – обозначает материальное начало. На
  материальном базируется построение дальнейшего опыта;
• Уруз – энергия преодоления препятствий.
  Позволяет идти дальше на пути к познанию;
• Турисаз – защищает на избранном пути;
• Дааз или Дагаз – завершает начинание. Это руна
  перехода в новое состояние, символизирует перемены.

Руны в кругу повторяются, что символизирует непрерывный
жизненный цикл и постоянное самосовершенствование носителя.

Свойства равностороннего треугольника:

1. В равностороннем треугольнике все стороны равны между собой.

2. В равностороннем треугольнике углы равны и составляют 60°.

3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.

В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.

В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.

Рис. 2. Равносторонний треугольник

АK = BF = CD

4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.

Рис. 3. Равносторонний треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.

6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.

Рис. 4. Равносторонний треугольник

AO : OK = BO : OА = CO : OD = 2 : 1

Числовой символизм валькнута

Числа играют очень важную роль во всех языческих религиях. Числовой символизм, соответственно, присущ и скандинавскому язычеству.

Числа, отраженные в изображении «узла павших» — это 3 и 9. Они имеют свое собственные сакральное значение. 9 – это число миров в скандинавской мифологии:

1. Мир богов или Асгард.
2. Мир людей или Мидгард.
3. Мир умерших или Хельхейм.
4. Мир ванов или Ванахейм.
5. Мир великанов или Йотунхейм.
6. Мир светлых альвов или Альвхейм.
7. Мир огненных великанов или Муспельхейм.
8. Мир ледяных великанов или Нифльхейм.
9. Мир карликов или Свартальфахейм.

Также 9 – число ветвей мирового ясеня Иггдрассиля (по одному
на каждый мир). 9 ветвей – основа рун старшего алфавита (футарка). 3 – число
норн (богинь судьбы), отражающее настоящее, прошлое и будущее.

Фигура треугольник в трейдинге

Теперь, когда мы обсудили большинство важных моделей треугольников, посмотрим, как их можно использовать в своей торговле.

На графике показаны пять примеров треугольников и их потенциальные результаты.

График начинается с большого симметричного треугольника. Цена создает три убывающие вершины и три увеличивающиеся основания на графике. Стрелка в начале треугольника измеряет его размер. Как видите, такая же стрелка применяется, когда цена преодолевает верхний уровень треугольника и указывает на потенциальную цель модели, которая фиксируется через неделю.

Между тем, на пути к повышению цены создается график восходящего клина. Как мы уже говорили, восходящий клин имеет медвежий потенциал. При пробое нижнего уровня клина мы замечаем небольшую коррекцию.

В конце бычьей тенденции цена создает еще один симметричный треугольник. Позже цена пробивает нижний уровень и завершает размер фигуры.

При снижении цены возникает медвежий вымпел. Это консолидация после первого импульса медвежьего тренда. Далее цена пробивает нижний уровень вымпела. На пути вниз мы видим, что цена завершает первую цель, которая равна размеру вымпела.

Затем цена создает модель разворота с двойным дном и переключается на бычье направление. На пути вверх ценовое действие возникает расширяющийся треугольник

Обратите внимание, что верхний и нижний уровни шаблона увеличиваются. В этом случае ожидаемое движение цены является медвежьим и должно быть равным размеру паттерна

[править] Точки и линии, связанные с треугольником

Есть сотни различных построений для определения особых точек внутри треугольника, которые удовлетворяют некоторым уникальным условиям. Часто необходимо построить три прямые, связанные аналогично с тремя сторонами (вершинами, углами) треугольника и тогда убедиться, что они пересекаются в одной точке. Важным инструментом для проверки этого является теорема Чевы, которая дает критерии для определения конкурентности прямых. Подобно этому, линии, связанные с треугольником часто строятся после проверки, три аналогичным образом полученные точки является коллинеарными — теорема Менелая дает для этого случая общий критерий. В этом разделе приведены только такие построения, которые наиболее часто встречаются.

Центр описанной окружности.

Срединный перпендикуляр треугольника — это перпендикуляр, который проходит посередине стороны треугольника. Три срединных перпендикуляра пересекаются в одной точке, которая является центром описанной окружности. Диаметр описанной окружности можно определить из теоремы синусов.

Исходя из теоремы Фалеса, можно утверждать, что если центр описанной окружности расположен на одной из сторон треугольника, тогда противоположный угол прямой. Более того, если центр описанной окружности находится внутри треугольника, то треугольник остроугольный, а если наружу, то треугольник тупоугольный.

Три высоты треугольника пересекаются в ортоцентре.

Высота треугольника — прямая, проведенная из вершины и перпендикулярная к противоположной стороне или к продолжению противоположной стороны. Эта сторона называется основанием треугольника. Точка пересечения стороны и перпендикуляра называется основой перпендикуляра. Длина высоты — это расстояние от вершины к основанию треугольника. Три высоты пересекаются в одной точке, которая называется ортоцентром треугольника. Ортоцентр лежит внутри треугольника (и соответственно все основания перпендикуляров лежат в треугольнике) тогда и только тогда, когда треугольник не тупоугольный.

На пересечении двух биссектрис треугольника находится центр вписанной окружности.

Биссектриса треугольника — это прямая, проведенная через вершину, которая делит соответствующий угол на две равные части. Три биссектрисы пересекаются в одной точке, инцентре, центре вписанной в треугольник окружности. Вписанная окружность — это круг, который лежит внутри треугольника и примыкает к трем его сторонам. Кроме того, есть еще три важных круга, внешние вписанные; они лежат за пределами треугольника и соприкасаются с одной его стороной, а также к продолжению других двух. Центры внутреннего и внешних вписанных кругов образуют ортоцентрическую систему.

Барицентр — центр масс треугольника.

Медиана треугольника — это прямая, проведенная через вершину и середину противоположной стороны и делящая треугольник на две одинаковых площади. Три медианы пересекаются в одной точке, которая называется центроидом треугольника. Эта точка также центр масс треугольника: если бы треугольник был сделан из дерева, то можно было бы держать равновесие держась за центроид. Центроид делит каждую медиану в соотношении 2:1, например расстояние между вершиной и центроидом вдвое больше, чем между центроидом и противоположной стороной.

Окружность девяти точек.

Средние точки трех сторон и основы трех высот лежат на одном круге, который называется кругом девяти точек треугольника. Остальные три точки, из-за которых круг получил свое название, это середины той части высоты, лежащей между ортоцентром и вершиной. Радиус окружности девяти точек равен половине описанной окружности. Она соприкасается со вписанной окружностью (в точке Фейербаха) и с тремя внешними вписанными кругами.

Как выбрать тату-салон?

В связи с тем, что искусство татуировки за последние года получило широкое распространение, сегодня существует очень много тату-салонов. При этом далеко не всегда существует гарантия того, что обратившись в первый попавшийся салон, вы получите работу, которая была проведена качественно. В данном случае решением ситуации может стать только ответственный подход к подбору салона, где делают татуировки.

Отдавайте предпочтение в пользу тех тату-салонов, которые работают длительное время, имеют штат профессиональных специалистов с портфолио, а также имеющие хорошие отзывы от клиентов. Чем более ответственно вы подойдете к выбору тату-салона, тем большая вероятность того, что вы останетесь довольны работой, которая была выполнена.

Точка пересечения биссектрис треугольника

Теорема 2

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где $AM,\ BP,\ CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM\ и\ BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 3

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ,\ OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Теорема доказана.

Христианские варианты треугольника

В религиозной символике Средневековья появлялось много разновидностей подобных фигур:

1. Треугольник в сочетании с крестом символизировал смерть на кресте Иисуса за грехи человеческие, воскресение его Богом-Отцом, покаяние христиан и снисхождение Святого Духа.
2. Три рыбы, составляющие треугольник, означали: Иисус Христос, Сын Божий, Спаситель. Также они знаменовали Троицу.
3. Треугольник, содержащий греческие буквы Omicron, Omega и Nu. Эти буквы означают собой слова εγω ειμι ο ων, сказанные Богом Моисею из горящего куста (Исход 3:14), которые переводятся как «Я есть Сущий». Дословно фраза была взята из Септуагинты, древнегреческого перевода Ветхого Завета.
4. Три фигурки бегущих кроликов создают два треугольника, внутренний и внешний. Символ часто присутствовал как рельефный элемент архитектуры и деревянных деталей. Знак также знаменует Триединого Бога. Такое изображение встречается в настенной живописи древнего Египта и, возможно, тогда символизировало мужчину, женщину, потомство.